Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
Abstract
模型无关的元学习(meta-learning) 算法,兼容所有基于梯度下降训练的模型,适用于分类、回归和强化学习
通过对模型进行多任务训练(a variety of learning tasks),用少量训练样本解决新任务?
使用少量数据和训练就能在任务上得到很好的泛化性能
简单来说,MAML 赋予模型学习“如何学习”的能力,是的其在面对新任务时能够快速适应
Intro
算法核心:训练模型的初始参数,是的模型在之后遇到新的任务时,通过少量数据就能获得最大性能
与先前提出的元学习算法不同,此算法不增加学习参数数量,不约束模型架构
从特征学习的角度,MAML 算法过程,可以被视为构建了一种广泛使用于多种模型的内部表征(Internal representation)
从动力系统角度,这个学习过程可以被视为最大化新任务损失函数对参数的敏感性,只要敏感度够高,参数的微小变化就能使任务损失大幅提升
本文评估结果:监督分类任务中,MAML 优于专门为小样本学习的最先进方法(17 年),在回归问题和强化学习中,性能远超直接使用预训练模型进行初始化的传统方法
[!NOTE]
这里的显著优于适用于存在任务变异性的场景中强化学习进程的预训练初始化,对于普通的回归问题,原文为(can also be readily applied to)
Model-Agnostic Meta-Learning
这玩意通常在小样本学习的理论框架下
Meta-Learning Problem Set-Up
考虑一个模型$f$,将观测$x$映射到$a$,因为框架是通用的,所以需要通用任务概念
$$
\mathcal{T} = \left{ \mathcal{L}(\mathbf{x}_1, \mathbf{a}_1, \ldots, \mathbf{x}_H, \mathbf{a}_H),\ q(\mathbf{x}1),\ q(\mathbf{x}{t+1} \mid \mathbf{x}_t, \mathbf{a}_t),\ H \right}
$$
其中,包含一个损失函数$\mathcal{L}$,初始观测分布$q(\mathbf{x}1)$,转移分布$q(\mathbf{x}{t+1} \mid \mathbf{x}_t, \mathbf{a}_t)$,和情节长度$H$
独立同分布问题中,长度$H = 1$,模型在每个时间步选择一个$a$来生成长度为$H$的样本,损失函数提供任务特定的反馈
在元学习场景中,考虑一个任务分布$p(\mathcal{T})$,模型需要尽快适应这个新的分布
A Model-Agnostic Meta-Learning Algorithm
模型在新任务上使用基于梯度的规则进行微调,我们使用同样的方式学习一个模型,目标是找到对任务变化敏感的模型参数
这里的参数指的是内部参数,而不是超参数
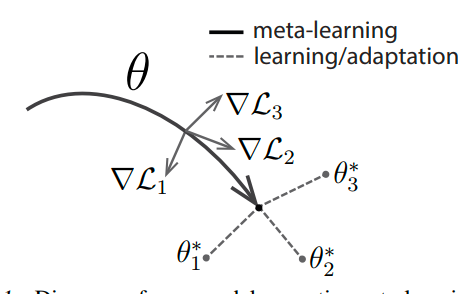
有一下两个假设
- 模型由$\theta$参数化
- 损失函数足够平滑
这里的损失通过任务的$\mathcal{L}$来计算,而$\theta$指代模型的内部参数,通过梯度下降更新
$$
\theta’i = \theta - \alpha \nabla{\theta}\mathcal{L}_{\mathcal{T}i}(f{\theta})
$$
本节考虑一次梯度更新的情况,多次也行,反正就是计算单个任务的较优内部参数
训练方式就是优化其在不同任务上对应的性能,即最小化代价函数
$$
\min_{\theta} \sum_{\mathcal{T}i \sim p(\mathcal{T})} \mathcal{L}{\mathcal{T}i} (f{\theta_i’}) = \sum_{\mathcal{T}i \sim p(\mathcal{T})} \mathcal{L}{\mathcal{T}i} (f{\theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)})
$$
通过随机梯度下降(SGD)执行优化迭代如下
$$
\theta \leftarrow \theta - \beta \nabla_{\theta} \sum_{\mathcal{T}{i} \sim p(\mathcal{T})} \mathcal{L}{\mathcal{T}{i}}(f{\theta_{i}^{\prime}})
$$
有形式化算法

对于单个损失的计算,使用了验证集和训练集
这里的梯度更新实际上涉及梯度的梯度,所以需要进行一次额外的反向传播,大多数库都支持
也有一种省略该传播的近似
实际应用和实现先不看了